电磁流量计的电极与励磁线圈不对称误差分析

摘 要：本文从基本理论出发，对电磁流量计的电极和励磁线圈在实际制造中可能的不对称问题进行研究，求出响应的电势和磁势的分布，并进行了定量分析，得到由此引起的测量误差。

关键字：电磁流量计 非对称 测量误差

    0 引言

    电磁流量计是一种重要的测量导电性液体体积流量的仪表。在实际制造中，如果流量计本身的电极和励磁线圈存在不对称偏差，将对测量结果造成一定的影响。但该方面所见文献较少，王国强研究了电磁流量计中的非对称流动问题产生的测量误差^[1]，张小章等研究气泡引起的不对称误差^[2]。本文对电极和线圈可能存在的位置偏差情况进行数值分析，并对所带来的测量误差进行初步探讨。

    1 电磁流量计基本理论

    描述电磁流量计的积分式由Bevir在1970年给出：

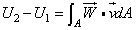            （1）

    其中：U₂-U₁是电极1、2之间的电势差；A表示对所有的空间积分；为流体的速度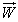；称为矢量权函数，它是一个只由电磁流量计本身结构决定的量，其表达式为：

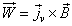                       （2）

    而且：

         （3）

    G和F分别是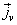和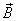的标量势，它们满足Laplace方程：

           （4）

    2 方程的求解和计算

    考虑二维平面上电磁流量计的横截面，如图1所示。它的边界是一圆周，半径为r₀。两个电极分别在管道的两侧，其尺寸可以视为一个很小的几何点，该点的电势G是一个脉冲函数，所以在极坐标下G的边界条件可表示为：

    G（r₀，θ）= f₁（θ）= δ（θ - θ₁） + δ（θ - θ₂ + π）      （5）

    其中θ₁，θ₂决定两个相对电极的位置。

    两个励磁线圈分别在圆域边界上下。磁势F随励磁线圈的分布分别取值0、1和-1，因此极坐标下F的边界条件可表示为

                      （6）

    其中角α₁，α₂，α₃，α₄决定励磁线圈的位置。在对称情况下α₁=α₂=α₃=α₄。

    式（4）式（6）是两组有定解条件的二维圆域拉普拉斯方程。用分离变量法对其求解，分别解得：

                  （7）

                            （8）

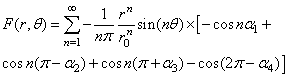                       （9）

    3 结果和分析

    3.1 电极位置偏差影响

    分别取3种情况下电势G分布如图2（a）、（b）、（c）所示。

    3.2 励磁线圈几何尺寸的影响

    分别3种情况下磁势F分布，如图3（a）、（b）、（c）所示。

    从图2和图3中可以比较直观了解电极和励磁线圈安装不对称情况下电势和磁势分布的具体情况。然而，要进一步了解这些因素对测量的影响，需要建立电极或线圈位置偏离与测量误差的关系，这对流量计的设计以及使用都有着更重要的意义。因此，定义以下量：

              （10）

    其中，δ₁，δ₂测量误差；G₀、F₀为完全对称情况下的电势和磁势；A为圆域面积。根据式（10）对电极和线圈的不同偏差情况进行计算，结果见图4（a）（b）。

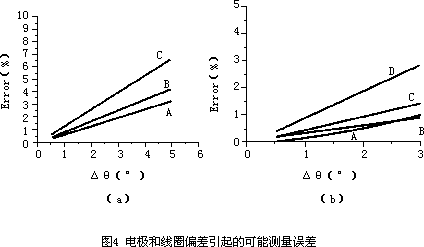
    图4（a）中：A表示右电极偏一定角度；B表示左右电极同方向偏离相同角度；C表示左右电极反方向偏离相同角度；图4（b）中：A表示上线圈偏一定角度；B表示上下线圈反方向偏离相同角度；C表示下线圈偏大；D表示下线圈偏小。

    从图中可见，电极位置变动对势G的影响较大，两个电极反向偏离时势场的变化最大、同向偏离次之，单电极偏离的影响最小。励磁线圈的偏离分两种情况，一种是励磁线圈仅在圆周上移动、长度不变。该类变化中上、下线圈同向偏离导致的变化量最大，单线圈偏离次之，反向偏离最小。另一种是励磁线圈不移动，仅在角位置上放大或缩小，计算结果显示线圈缩小对势场的影响更大。

    4 结论

    1）求得电磁流量计中电极和励磁线圈存在不对称偏差情况下的电势及磁势分布解析解。
    2）对不同的电极和励磁线圈在制造中可能发生的角向偏差情况进行数值模拟，得到电极和线圈位置变化对测量结果的影响规律。比如，电极的角位置偏差可能产生的测量误差大约为每度1.2%，而线圈的角位置偏差引起大约为每度0.7%误差。

    在进一步的工作中，可以采用三维理论模型，更深入地研究电极与励磁线圈径向位置发生偏差时的影响等。